معرفی
بسیاری از مدل‌های مسائل حمل‌ونقل صنعتی این فرض را می‌دهند که مشکل از نظر کروی متقارن است. این فرض از اهمیت زیادی برخوردار است زیرا دو مختصات فضایی را حذف می‌کند و یک مشکل 1 بعدی ایجاد می‌کند که از نظر محاسباتی سریع است و نیاز به حافظه بسیار کمی دارد. برخی از کاربردهایی که مفروضات تقارن کروی مفید هستند عبارتند از:
• | واکنش و انتشار در گلوله های کاتالیزوری در راکتورهای شیمیایی |
• | انتقال حرارت و جرم در پردازش گلوله های سنگ آهن ارتقا یافته |
• | هر فرآیند دیگری که در مهره هایی که تقریباً کروی هستند اتفاق می افتد |
برای اینکه تقارن کروی معتبر باشد، مفروضات زیر باید اعمال شوند:
• | حوزه محاسباتی شکل کروی دارد |
• | شرایط مرزی محیط بیرونی با موقعیت روی سطح تغییر نمی کند، یعنی با زوایای فضایی θ و تغییر نمی کند.  |
• | در هر زمان معین برای یک مسئله وابسته به زمان، خواص مواد فقط به فاصله شعاعی از مرکز، r و نه به زوایای فضای θ و نه بستگی دارد.  |
• | برای یک مسئله وابسته به زمان، شرط اولیه فقط به فاصله شعاعی از مرکز، r بستگی دارد و نه به زوایای فضایی θ و  |
تعریف مدل
مثال زیر فرآیند گرمایش گذرا اولیه یک قطعه سنگ معدن مگنتیت را شبیه سازی می کند. این اولین گام در فرآیند ساخت گلوله های سنگ معدن هماتیت، یک ماده اولیه مهم برای صنعت فولاد است.
در طول گرمایش اولیه گلوله مگنتیت، دما در محدوده ای قرار دارد که به شما امکان می دهد هر گونه تغییر فاز رطوبت را نادیده بگیرید. بنابراین می توان از یک معادله انتقال حرارت گذرا با خواص ثابت در تقارن کروی استفاده کرد. همچنین می توانید معادله را برای پارامترسازی آسان شعاع مقیاس کنید.
شکل 1 تعدادی گلوله را به همراه یک پین فشاری به عنوان مرجع مقیاس نشان می دهد.
شکل 1: گلوله های هماتیت پس از خشک شدن و اکسیداسیون (محصول نهایی).
شکل نشان می دهد که این گلوله ها در واقع کاملاً کروی نیستند. با این وجود، این مدل از فرض تقارن کروی بهره می برد.
معادلات دامنه
با معادله انتقال حرارت وابسته به زمان شروع می شود
و با گسترش آن در مختصات قطبی کروی، معادله حاصل می شود
جایی که ρ چگالی است (kg/m 3 )، cp ظرفیت گرمایی (J/(kg·K))، k نشان‌دهنده هدایت حرارتی (W/(m·K))، و Q یک منبع حرارت داخلی است. (W/m 3 ). علاوه بر این، r ، θ و 
مختصات فضایی هستند.
مختصات فضایی هستند.با فرض یک کره کامل به شعاع Rp و بدون تغییر دما با زوایای فضایی متفاوت، یا
برای جلوگیری از تقسیم بر صفر در r = 0 ، که باعث مشکلات عددی می شود، این معادله را در r 2 ضرب کنید.
(1)
استفاده از مختصات شعاعی بدون بعد 
با مقیاس گذاری معادله این امکان را فراهم می کند که شعاع گلوله را بدون تغییر یا پارامتر اندازه هندسی 1 به سرعت تغییر دهید . معرفی مختصات بدون بعد
با مقیاس گذاری معادله این امکان را فراهم می کند که شعاع گلوله را بدون تغییر یا پارامتر اندازه هندسی 1 به سرعت تغییر دهید . معرفی مختصات بدون بعد
و جایگزینی در معادله 1 منجر به
(2)
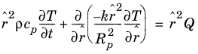
در دامنه زیر:
به روشی مشابه، می توان معادلات مشابه معادله 2 را برای جریان محیط متخلخل، مشکلات انتشار-واکنش و غیره استخراج کرد.
مدل از داده های مادی زیر استفاده می کند:
سمبل | نام | ارزش |
r | تراکم | 2000 کیلوگرم بر متر مکعب |
ج ص | ظرفیت گرمایی | 300 J/(kg·K) |
ک | رسانایی | 0.5 W/(m·K) |
R p | شعاع گلوله | 0.005 متر |
س | منبع گرما | 0W/ m3 |
شرایط مرزی و شرایط اولیه
به دلیل تقارن در مورد r = 0 ، شار صفر در این نقطه وجود دارد، به این معنی 
.
.در سطح، 
از یک عبارت گرمایش همرفتی با ضریب انتقال حرارت، h s (W/(m 2 ·K)) برای هجوم گرما (W/m 2 ) استفاده می‌کنید:
از یک عبارت گرمایش همرفتی با ضریب انتقال حرارت، h s (W/(m 2 ·K)) برای هجوم گرما (W/m 2 ) استفاده می‌کنید:
این عبارت یک گاز داغ با دمای T ext را توصیف می کند که در اطراف گلوله جریان دارد. Text در 95 درجه سانتیگراد انتخاب شده است. ضریب انتقال حرارت روی 1000 W/ ( m 2 ·K) تنظیم شده است. شرایط اولیه روی 25 درجه سانتیگراد تنظیم شده است.
نتایج
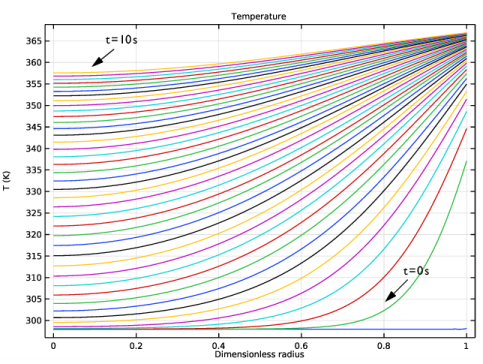
شکل 2: پروفیل های دما از t = 0 تا t = 10 s.
شکل 2 پروفیل های دما را از 0 تا 10 ثانیه نشان می دهد. هر خط نشان دهنده افزایش 0.5 ثانیه از خط قبل است. از بالاترین خط مشخص است که مرکز گلوله در 10 ثانیه به حالت ثابت نرسیده است. همچنین می توانید تکامل زمانی دما را در مرکز گلوله ترسیم کنید.
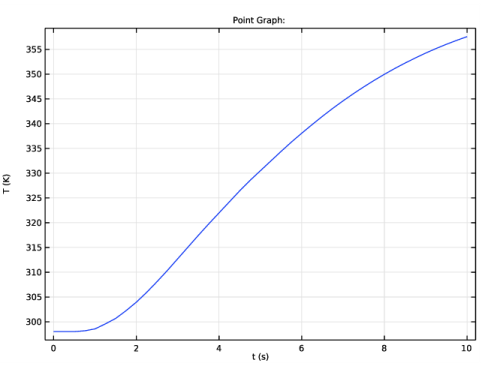
شکل 3: تکامل زمانی دما در مرکز یک گلوله با شعاع R p = 5 میلی متر.
شکل 3 با وضوح بیشتری نشان می دهد که فرآیند هنوز چقدر باید طول بکشد تا به حالت پایدار برسد. گام بعدی جالب ، آزمایش با شعاع ذرات مختلف، Rp و زمان‌های گرمایش متفاوت است.
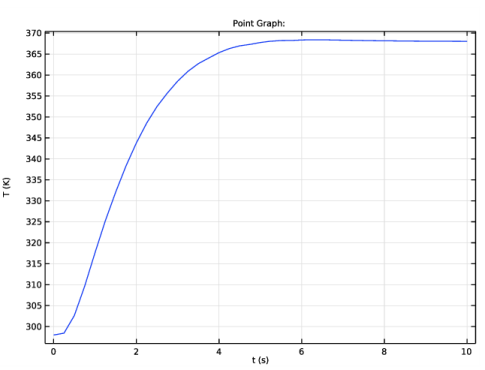
شکل 4: تکامل زمانی در مرکز یک گلوله با شعاع R p = 2.5 میلی متر.
صرفاً تا حدودی کاهش شعاع به مدل اجازه می دهد در عرض 7 ثانیه به حالت پایدار برسد.
نکاتی درباره پیاده سازی COMSOL
برای اجرای معادله 2 و شرایط مرزی این مسئله، از نسخه وابسته به زمان 1 بعدی رابط PDE فرم عمومی استفاده کنید:
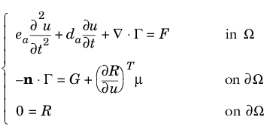
مختصات فضا در مدل است . به دلایل تایپی، ما از rh در این مدل برای ” r -hat” استفاده می کنیم. با شناسایی فرم کلی با معادله 2 ، تنظیمات زیر معادله صحیح را ایجاد می کند:
. به دلایل تایپی، ما از rh در این مدل برای ” r -hat” استفاده می کنیم. با شناسایی فرم کلی با معادله 2 ، تنظیمات زیر معادله صحیح را ایجاد می کند:ضریب | اصطلاح |
e a | 0 |
د الف |  |
C (بردار شار) |  |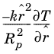
F (اصطلاح منبع) | 0 |
هنگام تنظیم شرایط مرزی هجوم گرما روی سطح گلوله باید مراقب باشید. h s ( T ext − T ) = k ∂ T / ∂ r روی سطح، بنابراین باید G را بر این اساس جبران کنید:
مسیر کتابخانه برنامه: COMSOL_Multiphysics/Equation_Based/Spherically_Symmetric_transport
دستورالعمل مدلسازی
از منوی File ، New را انتخاب کنید .
جدید
در پنجره جدید ، روی 
Model Wizard کلیک کنید .
Model Wizard کلیک کنید .مدل جادوگر
1 | در پنجره Model Wizard ، روی  1D کلیک کنید . |
2 | در درخت انتخاب فیزیک ، ریاضیات> رابط های PDE> فرم عمومی PDE (g) را انتخاب کنید . |
3 | روی افزودن کلیک کنید . |
4 | در جدول متغیرهای وابسته ، تنظیمات زیر را وارد کنید: |
تی |
5 |  روی مطالعه کلیک کنید . |
6 | در درخت انتخاب مطالعه ، General Studies>Time Dependent را انتخاب کنید . |
7 |  روی Done کلیک کنید . |
ریشه
1 | در پنجره Model Builder ، روی گره ریشه کلیک کنید. |
2 | در پنجره تنظیمات گره ریشه ، بخش Unit System را پیدا کنید . |
3 | از لیست سیستم واحد ، هیچکدام را انتخاب کنید . |
معادلات در این مدل با استفاده از مختصات شعاعی بدون بعد داده شده است. خاموش کردن پشتیبانی واحد از هشدارهای مربوط به استفاده ناسازگار از واحدها جلوگیری می کند.
تعاریف جهانی
پارامترهای 1
1 | در پنجره Model Builder ، در قسمت Global Definitions روی Parameters 1 کلیک کنید . |
2 | در پنجره تنظیمات برای پارامترها ، بخش پارامترها را پیدا کنید . |
3 | در جدول تنظیمات زیر را وارد کنید: |
نام | اصطلاح | ارزش | شرح |
rho | 2000 | 2000 | چگالی (kg/m^3) |
cp | 300 | 300 | ظرفیت گرمایی (J/(kg*K)) |
ک | 0.5 | 0.5 | هدایت حرارتی (W/(m*K)) |
Rp | 0.005 | 0.005 | شعاع گلوله (متر) |
Qs | 0 | 0 | منبع حرارت (W/m^3) |
hs | 1000 | 1000 | ضریب انتقال حرارت (W/(m^2*K)) |
متن | 368 | 368 | دمای خارجی (K) |
تینی | 298 | 298 | مقدار اولیه (K) |
هندسه 1
فاصله 1 (i1)
1 | در پنجره Model Builder ، در قسمت Component 1 (comp1) روی Geometry 1 کلیک راست کرده و Interval را انتخاب کنید . |
2 | در پنجره تنظیمات برای فاصله ، روی  ساخت همه اشیاء کلیک کنید . |
فرم عمومی PDE (G)
فرم عمومی PDE 1
1 | در پنجره Model Builder ، در قسمت Component 1 (comp1)>General Form PDE (g) روی General Form PDE 1 کلیک کنید . |
2 | در پنجره تنظیمات برای فرم عمومی PDE ، بخش Conservative Flux را پیدا کنید . |
3 | در قسمت متن Γ ، -k*x^2/Rp^2*Tx را تایپ کنید . |
4 | قسمت Source Term را پیدا کنید . در قسمت متن f ، x^2*Qs را تایپ کنید . |
5 | قسمت Damping یا Mass Coefficient را پیدا کنید . در قسمت متن d a ، x^2*rho*cp را تایپ کنید . |
توجه داشته باشید که Tx نحو COMSOL Multiphysics برای مشتق جزئی متغیر T با توجه به مختصات x است .
مقادیر اولیه 1
1 | در پنجره Model Builder ، روی مقادیر اولیه 1 کلیک کنید . |
2 | در پنجره تنظیمات برای مقادیر اولیه ، قسمت مقادیر اولیه را پیدا کنید . |
3 | در قسمت متن T ، Tinit را تایپ کنید . |
شار/منبع 1
1 | در نوار ابزار Physics ، روی  Boundaries کلیک کنید و Flux/Source را انتخاب کنید . |
2 | فقط مرز 1 را انتخاب کنید. |
شار/منبع 2
1 | در نوار ابزار Physics ، روی  Boundaries کلیک کنید و Flux/Source را انتخاب کنید . |
2 | فقط مرز 2 را انتخاب کنید. |
3 | در پنجره تنظیمات برای Flux/Source ، بخش Boundary Flux/Source را پیدا کنید . |
4 | در قسمت متن g ، x^2/Rp*hs*(Text-T) را تایپ کنید . |
مش 1
مقیاس 1
1 | در نوار ابزار Mesh ، روی  More Attributes کلیک کنید و Scale را انتخاب کنید . |
2 | در پنجره تنظیمات برای مقیاس ، بخش مقیاس را پیدا کنید . |
3 | در قسمت متنی مقیاس اندازه عنصر ، 0.4 را تایپ کنید . |
لبه 1
1 | در نوار ابزار Mesh ، روی  Edge کلیک کنید . |
2 | در پنجره تنظیمات Edge ، روی  Build All کلیک کنید . |
مطالعه 1
مرحله 1: وابسته به زمان
1 | در پنجره Model Builder ، در بخش مطالعه 1 ، روی Step 1: Time Dependent کلیک کنید . |
2 | در پنجره تنظیمات مربوط به زمان وابسته ، قسمت تنظیمات مطالعه را پیدا کنید . |
3 | در قسمت متن زمان خروجی ، range(0,0.25,10) را تایپ کنید . |
4 | در نوار ابزار صفحه اصلی ،  روی محاسبه کلیک کنید . |
نتایج
نمودار پیش فرض دما را در مقابل شعاع بدون بعد برای همه زمان ها در بازه مشخص شده نشان می دهد.
گروه طرح 1 بعدی 1
1 | در پنجره Model Builder ، در قسمت Results روی 1D Plot Group 1 کلیک کنید . |
2 | در پنجره تنظیمات برای گروه طرح 1 بعدی ، برای گسترش بخش عنوان کلیک کنید . |
3 | از لیست نوع عنوان ، دستی را انتخاب کنید . |
4 | در قسمت متن عنوان ، Temperature را تایپ کنید . |
5 | قسمت Plot Settings را پیدا کنید . |
6 | چک باکس x-axis label را انتخاب کنید . در فیلد متن مرتبط، Dimensionless radius را تایپ کنید . |
7 | کادر بررسی برچسب محور y را انتخاب کنید . در قسمت متن مرتبط، T (K) را تایپ کنید . |
8 | در نوار ابزار 1D Plot Group 1 ، روی  Plot کلیک کنید . |
برای رسم تکامل زمانی دما در مرکز گلوله به شعاع 5 میلی متر ( شکل 3 )، مراحل زیر را دنبال کنید.
گروه طرح 1 بعدی 2
در نوار ابزار صفحه اصلی ، روی Add Plot Group کلیک کنید و 1D Plot Group را انتخاب کنید .
Add Plot Group کلیک کنید و 1D Plot Group را انتخاب کنید .نمودار نقطه 1
1 | روی 1D Plot Group 2 کلیک راست کرده و Point Graph را انتخاب کنید . |
2 | فقط مرز 1 را انتخاب کنید. |
گروه طرح 1 بعدی 2
1 | در پنجره Model Builder ، روی 1D Plot Group 2 کلیک کنید . |
2 | در پنجره Settings for 1D Plot Group ، قسمت Plot Settings را پیدا کنید . |
3 | چک باکس x-axis label را انتخاب کنید . در قسمت متن مرتبط، t (s) را تایپ کنید . |
4 | کادر بررسی برچسب محور y را انتخاب کنید . در قسمت متن مرتبط، T (K) را تایپ کنید . |
5 | در نوار ابزار 1D Plot Group 2 ، روی  Plot کلیک کنید . |
اکنون در قسمت Parameters شعاع گلوله را به 2.5 میلی متر تغییر دهید و تاثیر آن را بر روی تکامل زمانی دما در مرکز گلوله مشاهده کنید.
تعاریف جهانی
پارامترهای 1
1 | در پنجره Model Builder ، در قسمت Global Definitions روی Parameters 1 کلیک کنید . |
2 | در پنجره تنظیمات برای پارامترها ، بخش پارامترها را پیدا کنید . |
3 | در جدول تنظیمات زیر را وارد کنید: |
نام | اصطلاح | ارزش | شرح |
Rp | 0.0025 | 0.0025 | شعاع گلوله (متر) |
مطالعه 1
در نوار ابزار صفحه اصلی ، روی محاسبه کلیک کنید .
روی محاسبه کلیک کنید .نتایج
گروه طرح 1 بعدی 2
نمودار حاصل باید مانند شکل 4 باشد .
1 | در پنجره Model Builder ، در قسمت Results روی 1D Plot Group 2 کلیک کنید . |
2 | در نوار ابزار 1D Plot Group 2 ، روی  Plot کلیک کنید . |
1
توجه داشته باشید که مقیاس بندی متغیرها برای بدست آوردن مسائل شرطی شده به خوبی در COMSOL Multiphysics ضروری نیست زیرا حل کننده ها از مقیاس بندی متغیر خودکار استفاده می کنند.
