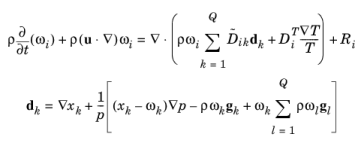در یک مخلوط چند جزئی، شار جرم نسبت به سرعت میانگین جرمی ، j i ، را می توان با معادلات فیک تعمیم یافته تعریف کرد ( مرجع 1 ):
(6-41)
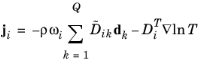
در معادله 6-41 :
• |
• | T (واحد SI: K) دما است |
• |
• | d k (واحد SI: 1/m) نیروی محرکه انتشاری است که بر روی گونه k عمل می کند . |
برای مخلوطهای گازی ایدهآل، نیروی محرکه انتشاری است ( مرجع 1 )
(6-42)
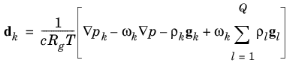
جایی که
• | c (واحد SI: mol/m 3 ) غلظت مولی کل است |
• | Rg ثابت گاز جهانی 8.314 J/(mol·K) است . |
• | p (واحد SI: Pa) فشار کل است |
• | p k (واحد SI: Pa) فشار جزئی است و |
• | ρ k (واحد SI: kg/m 3 ) چگالی گونه k است و |
• | g k (واحد SI: m/s 2 ) نیروی خارجی (به ازای واحد جرم) است که بر گونه k تأثیر می گذارد . در مورد یک گونه یونی، نیروی خارجی به دلیل میدان الکتریکی ایجاد می شود. |
وقتی یک نیروی خارجی به طور یکسان بر همه گونه ها اعمال می شود (مانند گرانش)، دو عبارت آخر ناپدید می شوند. |
همانطور که در معادله 6-41 و معادله 6-42 مشاهده می شود ، شار انتشاری کل برای گونه ها به گرادیان غلظت ها، دما و فشار همه گونه ها و همچنین هر نیروی خارجی بر روی گونه های منفرد بستگی دارد.
با استفاده از قانون گاز ایده آل، p = c·R g ·T ، و تعریف فشارهای جزئی، pk = x k p ، معادله را می توان به صورت زیر نوشت:
(6-43)
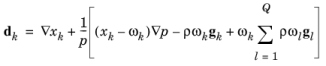
کسر مول x k به دست می آید
(6-44)
و میانگین جرم مولی M (واحد SI: kg/mol) توسط
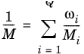
هنگام استفاده از مدل انتشار ماکسول-استفان، معادلات حمل و نقل برای جرم گونه است
(6-45)