اکثر مسائل حل شده با COMSOL Multiphysics در دنیای واقعی سه بعدی (3D) هستند. در بسیاری از موارد، حل یک مسئله دوبعدی (2 بعدی) که نزدیک به مسئله واقعی یا معادل آن است، کافی است.
شروع یک پروژه مدلسازی با ساخت یک یا چند مدل دو بعدی قبل از رفتن به مدل سه بعدی تمرین خوبی است. |
این به این دلیل است که مدلهای دوبعدی اصلاح آسانتر و سریعتر حل میشوند. بنابراین، اشتباهات مدلسازی هنگام کار در دو بعدی بسیار آسان تر است. هنگامی که مدل دو بعدی تأیید شد، در موقعیت بسیار بهتری برای ساخت یک مدل سه بعدی هستید.
مشکلات دو بعدی
در زیر راهنمای برخی از تقریب های متداول ساخته شده برای مسائل دو بعدی است. به یاد داشته باشید که مدل سازی در دو بعدی معمولاً هندسه سه بعدی را با این فرض نشان می دهد که هیچ چیز در بعد سوم تغییر نمی کند. |
مختصات کارتزین
در این حالت شما یک مقطع را در صفحه xy هندسه سه بعدی واقعی مشاهده می کنید. هندسه از نظر ریاضی تا بی نهایت در هر دو جهت در امتداد محور z گسترش یافته است ، با فرض عدم تغییر در طول آن محور. تمام جریان های ورودی و خارج از مرزها در واحد طول در امتداد محور z هستند . یک روش ساده شده برای بررسی این موضوع این است که فرض کنیم هندسه یک واحد طول از مقطع در امتداد محور z اکسترود شده است . جریان کل خارج از هر مرز از وجهی است که توسط مرز اکسترود شده ایجاد شده است (یک مرز در 2 بعدی یک خط است).
معمولاً دو رویکرد وجود دارد که منجر به یک نمای مقطعی دوبعدی از یک مشکل می شود:
• | هنگامی که مشخص شود که هیچ گونه تغییری از راه حل در یک بعد خاص وجود ندارد. |
• | هنگامی که مشکلی وجود دارد که در آن تأثیر گسترش محدود در بعد سوم می تواند نادیده گرفته شود. |
نیروهای الکترومغناطیسی روی سیمهای حامل جریان موازی : مسیر کتابخانه برنامه ACDC_Module/Introductory_Electromagnetic Forces/Morallel_wires |
هندسه دارای عرض محدود است اما مدل از اثرات (انتها) از وجوه موازی با مقطع چشم پوشی می کند زیرا قوی ترین نیروها بین وجوه عمود بر هم هستند (آنهایی که به صورت خطوط در مقطع دیده می شوند).
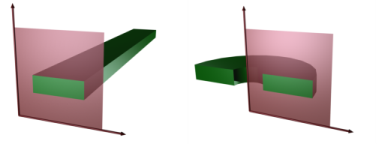
شکل 3-1: مقاطع عرضی و هندسه واقعی آنها برای مختصات دکارتی (سمت چپ) و مختصات استوانه ای (تقارن محوری).
تقارن محوری (مختصات استوانه ای)
اگر بتوان هندسه سه بعدی را با چرخاندن یک مقطع حول یک محور ساخت و هیچ تغییری در هیچ متغیری در حول محور چرخش رخ ندهد، می توان از رابط فیزیک متقارن محوری استفاده کرد. |
مختصات فضایی r و z نامیده می شوند که r شعاع است. جریان در مرزها در واحد طول در امتداد بعد سوم داده می شود. از آنجایی که این بعد یک چرخش است، باید تمام جریان ها را با α r ضرب کنید ، که α زاویه چرخش است (مثلا 2 π برای یک دور کامل).
عایق ولتاژ بالا : مسیر کتابخانه برنامه ACDC_Module/Devices,_capacitive/highvoltage_insulator |
متغیرهای فیلد دو بعدی
هنگام حل یک میدان برداری در دو بعدی، رابط فیزیک سه گزینه دارد: برای حل بردار خارج از صفحه، بردار درون صفحه یا بردار سه جزیی. بسته به انتخاب، گزینههای مشخصات منبع موجود در سطح دامنه، مرز، لبه و نقطه بر این اساس تغییر میکنند.
مشکلات سه بعدی
این بخش مسائلی را مورد بحث قرار می دهد که باید قبل از شروع به پیاده سازی یک مدل سه بعدی مورد توجه قرار گیرد. |
اگرچه COMSOL Multiphysics به طور کامل از هندسه های سه بعدی دلخواه پشتیبانی می کند، ساده کردن مشکل بسیار مهم است. این به این دلیل است که مشکلات سه بعدی به راحتی بزرگ می شوند و برای حل آنها به قدرت، حافظه و زمان بیشتری کامپیوتر نیاز دارند. زمان اضافی صرف شده برای ساده کردن یک مشکل احتمالاً هنگام حل آن به خوبی صرف می شود.
آیا امکان حل مشکل به صورت دو بعدی وجود دارد؟
با توجه به اینکه تقریب های لازم کوچک هستند، راه حل در دو بعدی دقیق تر است زیرا می توان از مش بسیار متراکم تری استفاده کرد. اگر این مورد قابل اجرا است، مشکلات دوبعدی را ببینید .
آیا وابستگی در یک جهت را می دانید تا بتوان آن را با یک تابع تحلیلی جایگزین کرد؟
شما می توانید از این روش برای تبدیل 3 بعدی به 2 بعدی یا برای تبدیل یک لایه به یک شرط مرزی استفاده کنید (به ساده سازی هندسه با استفاده از شرایط مرزی مراجعه کنید ).
آیا در هندسه و مدل تقارن وجود دارد؟
بسیاری از مسائل دارای هواپیماهایی هستند که راه حل در دو طرف هواپیما یکسان به نظر می رسد. یک راه خوب برای بررسی این موضوع، چرخاندن هندسه در اطراف صفحه است، برای مثال، با چرخاندن آن به سمت پایین در اطراف صفحه افقی. اگر تفاوتی بین این دو مورد در مورد هندسه، مواد و منابع مشاهده نکردید، سپس میتوانید هندسه زیر صفحه را حذف کنید. مرزهای ایجاد شده توسط مقطع بین هندسه و این صفحه نیاز به یک شرط مرزی تقارن دارند که در تمام رابط های فیزیک سه بعدی موجود است.
جریان های گردابی : مسیر کتابخانه برنامه ACDC_Module/Introductory_Electromagnetics/eddy_currents |




