شکل کلی و ضریب PDE ها در معادلات 16-1 و معادله 16-2 PDE ها را به شکل قوی مشخص می کند، به این معنا که آنها، در اصل، نیاز دارند که PDE در هر نقطه از هندسه برآورده شود. و برای اینکه این امکان پذیر باشد، همه اصطلاحات باید به اندازه کافی پیوسته باشند تا مشتقات و مقادیر نقطه ای کاملاً تعریف شده وجود داشته باشند. در بسیاری از موارد، پدیدههای طبیعی که یک PDE قصد مدلسازی را دارد، به بهترین وجه بهعنوان ناپیوسته توصیف میشوند و همچنین ممکن است حاوی عبارات منبعی باشند که فقط به عنوان مجموع در یک منطقه کوچک، بدون مقدار نقطهای کاملاً تعریف شده، تعریف میشوند.
در این شرایط، یک معادله ضعیف مدل فیزیک بهتری نسبت به PDEهای قویتر است. علاوه بر این، فرم ضعیف به ویژه برای گسسته سازی و حل عددی با استفاده از روش اجزای محدود مناسب است. یکی از دلایل این امر دقیقاً نیاز به تداوم کمتر در محلول است که فقط باید به اندازه کافی صاف روی هر عنصر مش به طور جداگانه باشد.
مثال: تبدیل از فرم عمومی به فرم ضعیف
به عنوان مثال، شکل کلی ارائه شده در معادله 16-1 ، به ویژه شکل ثابت معادله دامنه را در نظر بگیرید:
با فرض یک متغیر وابسته منفرد u ، یک تابع تست دلخواه متناظر υ را معرفی کنید . معادله را در این تابع تست ضرب کنید و روی دامنه ادغام کنید:
(16-5)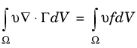
این معادله انتگرال به وضوح بیانیه ضعیف تری نسبت به معادله اصلی است، به ویژه زمانی که معادله 16-5 لازم است فقط برای همه توابع آزمایشی υ از یک کلاس محدود از توابع وجود داشته باشد. در روش اجزای محدود، توابع آزمون υ (و همچنین حل u ) معمولاً به مجموعه چند جمله ای های تکه ای با یک مرتبه معین روی هر عنصر مش محدود می شوند.
این چند جمله ای را می توان به صورت مجموع توابع شکل جداگانه نیز نوشت . بنابراین، شکل قوی اصلی PDE به یک معادله شکل ضعیف تبدیل میشود، که فقط باید به معنای انتگرال محلی در هر تابع شکل ارضا شود. وقتی تعداد توابع شکل را با پالایش مش یا افزایش ترتیب چند جمله ای افزایش می دهید، به طور همزمان فضای راه حل های u را کاهش می دهید که احتمالاً می تواند معادله 16-5 را برآورده کند . بنابراین، فرمولبندیهای المان محدود خوب و سازگار به سمت راهحل منفرد u که فرم قوی اصلی PDE را برآورده میکند، همگرا میشوند.
برای ساده کردن بیشتر حل معادله 16-5 ، انتگرال سمت چپ را می توان با استفاده از قانون گاوس با قطعات ادغام کرد:
(16-6)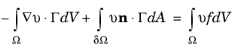
این دو مزیت اصلی دارد. اول از همه، حداکثر ترتیب مشتقات فضایی را کاهش می دهد. اگر Γ تابعی از گرادیان u باشد ، برای مثال Γ = − c ∇ u −α u + γ در شکل ضریب PDE، معادله ضعیف تبدیل شده اکنون فقط مشتقات مرتبه اول را در مقایسه با مشتقات مرتبه دوم در دارد. فرم قوی اصلی PDE. ثانیاً، مشخص می کند که شرایط مرزی طبیعی برای این معادله چیست. انتگرال دوم در سمت چپ ناپدید می شود اگر جزء طبیعی Γ در مرز ناپدید شود. متناوباً، اگر مقدار جزء نرمال مشخص باشد، به عنوان مثال به گونه ای که
(16-7)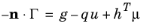
در δΩ ، این مقدار را می توان به عنوان یک شرط مرزی در معادله شکل ضعیف وارد کرد، که سپس تبدیل می شود
(16-8)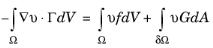
بنابراین این فرمول ضعیف نهایی فرم عمومی استاندارد PDE همچنین توضیح می دهد که چرا شرط مرزی نویمان در خط دوم معادله 16-1 به نظر می رسد.




