مشکلات آکوستیک فشار شامل حل تغییرات فشار آکوستیک کوچک p (همچنین p ‘ یا p 1 نامیده می شود ) در بالای فشار زمینه ثابت p 0 است . از نظر ریاضی، این نشان دهنده خطی سازی (بسط پارامتر کوچک) متغیرهای وابسته در اطراف مقادیر ساکن ساکن است.
معادلات حاکم برای مشکل جریان سیال بدون تلفات تراکم پذیر (بدون رسانش حرارتی و بدون ویسکوزیته) معادله بقای جرم (معادله پیوستگی)، معادله بقای تکانه (معادله اویلر) و معادله انرژی (معادله آنتروپی) است. اینها توسط:
(2-11)
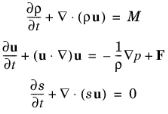
جایی که ρ چگالی کل است، p فشار کل، u میدان سرعت، s آنتروپی است، M و F عبارتهای منبع ممکن را نشان میدهند. در آکوستیک فشار کلاسیک، همه فرآیندهای ترمودینامیکی برگشت پذیر و آدیاباتیک فرض می شوند، یعنی فرآیندهای ایزنتروپیک. انبساط پارامتر کوچک بر روی یک سیال ثابت ( u 0 = 0 ) با چگالی ρ 0 (واحد SI: kg/m3 ) و در فشار p 0 (واحد SI: Pa) انجام می شود به طوری که:
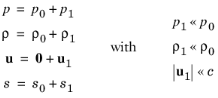
که در آن متغیرهای با زیرنویس 1 نشان دهنده تغییرات آکوستیک کوچک هستند (بسط مرتبه 1). با فرض صفر بودن آنتروپی اولیه s 0 ، آنگاه باقی می ماند و s 0 = 0. درج این مقادیر در معادلات حاکم و تنها حفظ عبارت های خطی در متغیرهای صوتی نتیجه می دهد.
(2-12)
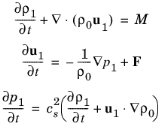
که در آن cs به عنوان سرعت (ایسنتروپیک) صوت (واحد SI: m/s) در آنتروپی ثابت s تشخیص داده می شود . آخرین معادله برای دیفرانسیل زمان فشار از معادله آنتروپی مشتق شده است، برای جزئیات بیشتر به پیشینه تئوری برای شاخه آکوستیک ترموویسکوز مراجعه کنید . برای پارامترهای ثابت مواد آخرین معادله به رابطه معمول کاهش می یابد
این عبارت شرط مفیدی را به دست می دهد که برای برقراری معادلات آکوستیک خطی باید برآورده شود:
زیرنویس ” s ” در زیر به همراه زیرنویس “0” در چگالی پسزمینه ρ 0 حذف میشود . در نهایت، تنظیم مجدد معادله 2-12 ، تغییر نام عبارات منبع، و حذف زیرنویس “1” معادله موج را برای امواج فشار در یک محیط بدون تلفات به دست میدهد.
(2-13)  .
.
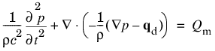 .
.در اینجا ρ (واحد SI: kg/m 3 ) به چگالی اشاره دارد و c (واحد SI: m/s) نشان دهنده سرعت صوت است. در این فرمول کلی معادله موج اسکالر، سرعت صوت و چگالی ممکن است به طور کلی به فضا وابسته باشند، برای مثال، از طریق وابستگی آنها به دمای پس زمینه. معادله شامل دو عبارت منبع اختیاری است:
• | منبع دامنه تک قطبی Q m (واحد SI: 1/s 2 ). این منبع با منبع جرمی در سمت راست معادله پیوستگی مطابقت دارد. |
• | منبع دامنه دوقطبی q d ( واحد SI: N/m 3 ). این منبع مربوط به منبع نیروی دامنه در سمت راست معادله تکانه است. |
ترکیب ρc2 مدول توده آدیاباتیک نامیده می شود که معمولاً Ks ( واحد SI: Pa) نشان داده می شود . مدول توده ای برابر است با ضریب تراکم پذیری آدیاباتیک βs = 1/ Ks = 1/ ρc2 (واحد SI: 1/Pa) .
در معادله 2-13، هم سرعت صوت c = c ( x ) و هم چگالی ρ = ρ ( x ) ممکن است به مختصات فضایی x وابسته باشند در حالی که مستقل از زمان هستند، یا فقط به آرامی در زمان تغییر می کنند (یعنی در مقیاس زمانی بسیار کندتر از تغییرات در سیگنال صوتی). اگر هر دو منبع دامنه روی صفر تنظیم شده باشند و چگالی در فضا ثابت باشد، می توانید معادله موج استاندارد را بازیابی کنید.
برخی از مراجع کلاسیک در مورد آکوستیک برای مطالعه بیشتر در Ref. 4 ، ر. 5 ، ر. 6 ، ر. 7 و Ref. 8 . |
یک مورد خاص مهم یک موج هارمونیک زمان است که فشار آن با زمان تغییر می کند
که در آن ω = 2 π f (rad/s) فرکانس زاویه ای و f (واحد SI: هرتز) فرکانس است. با فرض همان وابستگی زمانی هارمونیک برای عبارات منبع، معادله موج برای امواج صوتی به یک معادله هلمهولتز ناهمگن کاهش می یابد.
(2-14)  .
.
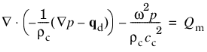 .
.در این معادله، زیرنویس « c » در چگالی و سرعت صوت به این اشاره دارد که ممکن است مقدار آنها مختلط باشد. رسانه های تلف کننده، مانند مواد متخلخل یا سیالات بسیار چسبناک، می توانند با استفاده از سرعت و چگالی صوت با ارزش پیچیده مدل سازی شوند. مجموعهای از این مدلهای سیال در The Pressure Acoustics، Frequency Domain Interface موجود است . میرایی در این مدلهای سیال بسته به منشأ فیزیکی میرایی، به طرق مختلف به فرکانس وابسته است. شرح مدلهای مختلف سیالات در نظریه مدلهای سیال معادل آورده شده است .
در حوزه زمان، فقط وابستگیهای فرکانس خاصی را میتوان مدلسازی کرد، که تعداد مدلهای سیال قابل استفاده در The Pressure Acoustics، Transient Interface را محدود میکند . یکی از راههای مدلسازی میرایی در حوزه زمان، معرفی یک عبارت مرتبه اول اضافی در مشتق زمانی برای محاسبه تضعیف امواج صوتی است.
(2-15)
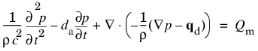
عبارت میرایی در معادله 2-15 در فرمولاسیون استاندارد PDE در فشار آکوستیک، رابط گذرا وجود ندارد، اما مربوط به منبع حوزه تک قطبی متناسب با مشتق زمانی فشار است. با این حال، این رویکرد در مدلهای سیال چسبناک و رسانای حرارتی که حاوی میرایی برای آکوستیک گذرا هستند استفاده نمیشود (به مدل سیال چسبناک ، مدل سیال رسانای حرارتی ، و مدل سیال رسانا و چسبناک نگاه کنید ). منشأ فیزیکی میرایی در اینجا با منبعی شبیه دوقطبی مطابقت دارد.
حتی زمانی که امواج صوتی در یک محیط بدون تلفات منتشر می شوند، تضعیف می تواند با تعامل با محیط اطراف در مرزهای سیستم رخ دهد. به ویژه، این امر در مورد شرایط مرزی امپدانس صدق می کند. |
روش دیگر، معادله هلمهولتز 2-14 را به عنوان یک PDE مقدار ویژه برای حل حالت های ویژه و فرکانس های ویژه در نظر بگیرید، به تحلیل فرکانس ویژه و حالت در بخش های متقارن محوری 2 بعدی و 1 بعدی در زیر مراجعه کنید.
برای حل معادلات حاکم، شرایط مرزی ضروری است. شرایط مرزی معمول مورد استفاده در آکوستیک عبارتند از:
• | مرز سخت صدا (دیوار) |
• | مرز نرم صدا (فشار آکوستیک صفر) |
• | فشار صوتی مشخص شده |
• | شتاب معمولی مشخص شده |
• | شرایط مرزی امپدانس (همچنین به نظریه مدلهای امپدانس مرزی مراجعه کنید ) |
• | تابش موج هواپیما |
• | تابش موج کروی |
• | تابش موج استوانه ای |




