نظریه الکترولیت
گره الکترولیت تعادل جریان را در الکترولیت تعریف می کند. معادله دامنه این است:
جایی که i l نشان دهنده بردار چگالی جریان است. در الکترولیت آزاد، منبع یا سینک شارژ وجود ندارد.
تعریف بردار چگالی جریان به فرمول معادله انتقال بار الکترولیت بستگی دارد، همانطور که در بالا در معادلات دامنه برای توزیع جریان اولیه و ثانویه و معادلات دامنه برای توزیع جریان سوم با استفاده از معادلات نرنست-پلانک و الکترونوترالیتی مورد بحث قرار گرفت .
|
نظریه الکترود متخلخل
الکترود متخلخل یک ماده مخلوط با یک فاز الکترود و یک فاز الکترولیت است. (یک مورد خاص از یک الکترود متخلخل، الکترود انتشار گاز است، همانطور که در یک پیل سوختی یافت می شود. این الکترودها حاوی یک فاز منفذ گازی هستند که برای انتقال بار بی اثر است.) برای مدل سازی یک الکترود متخلخل، دو تعادل جریان مجزا را طبق موارد زیر تعریف می کنیم. معادلات:
در این معادلات، i بردار چگالی جریان در الکترولیت را نشان میدهد، همانطور که در بالا در معادلات دامنه برای توزیع جریان اولیه و ثانویه و معادلات دامنه برای توزیع جریان سوم با استفاده از معادلات نرنست-پلانک و الکترونیوترالیتی مورد بحث قرار گرفت .
علاوه بر ترازهای جریان، لازم است معادلات موازنه جرم برای گونه های موجود در فاز الکترولیت برای مورد سوم نیز فرموله شود.
همچنین استفاده از رسانایی اصلاح شده و مقادیر پارامتر انتشار در یک الکترود متخلخل برای محاسبه کسر حجمی پایینتر فاز رسانا و فاصله انتقال طولانیتر به دلیل پیچ خوردگی منافذ معمول است.
تعادل جریان در الکترولیت منفذی و در ماتریس الکترود حاوی منابع و غرقها مطابق با واکنشهای انتقال بار است که در کاتالیزور الکترود انجام میشود. به عنوان مثال، اگر تنها یک واکنش انتقال بار در الکترود متخلخل انجام شود، معادلات دامنه به شرح زیر است:
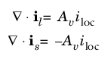
که در آن A v مساحت سطح خاص را نشان می دهد (بعد L 2 / L 3 )، و i loc چگالی جریان محلی، نرخ واکنش های انتقال بار را تعیین می کند، برای مثال مطابق با معادله باتلر-ولمر. برای روش های مختلف تعریف i loc به بیان جنبشی الکترود مراجعه کنید .
اگر الکترود متخلخل یک کاتد باشد، واکنش انتقال بار منبعی برای تعادل جریان در الکترود است، زیرا جریان را از الکترولیت منافذ دریافت می کند. واکنش انتقال بار پس از آن یک سینک برای تعادل جریان در الکترولیت منفذی است، زیرا جریان در یک واکنش کاتدی از الکترولیت منفذی به الکترود منتقل میشود.
منابع و سینکهای مربوطه در تعادلهای جاری که ناشی از واکنشهای انتقال بار هستند نیز با تعادل مواد برای گونههای باردار جفت میشوند. این بدان معنی است که بیان چگالی جریان محلی بالا نیز در ترازهای مواد به عنوان یک عبارت واکنش، Ri ، با استفاده از قوانین فارادی برای هر یک از گونه هایی که در واکنش های انتقال بار شرکت می کنند، گنجانده می شود.
|
نظریه واکنش های الکترود
واکنشهای انتقال بار که در یک رابط بین الکترود و حوزه الکترولیت رخ میدهند، یک شار جریان معمولی ایجاد میکنند که با مجموع تمام جریانهای واکنش برابر است.
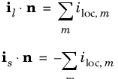
جایی که i loc ,m (A/m 2 ) چگالی جریان واکنش الکترود واکنش الکترود انتقال بار شاخص m است ، i بردار چگالی جریان در الکترولیت و i بردار چگالی جریان در الکترود است .
نظریه واکنش های الکترود متخلخل
برای یک الکترود متخلخل، چگالی جریان واکنش الکترود در مساحت سطح ضرب می شود تا منبع یا سینک در معادله دامنه تعادل جریان بر اساس:
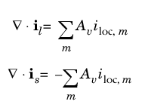
که در آن A v سطح ویژه الکتروکاتالیست است.
واکنش الکترود متخلخل |
نظریه الکترود
رسانایی الکترون در الکترود با استفاده از قانون اهم مدلسازی میشود. معادله دامنه به صورت زیر است:
جایی که i بردار چگالی جریان را با توجه به:
و جایی که σ s نشان دهنده هدایت الکتریکی و  s پتانسیل فاز رسانای الکترون (فلز) است.
s پتانسیل فاز رسانای الکترون (فلز) است.
نظریه چگالی جریان الکترولیت
چگالی جریان اعمال شده را می توان به عنوان جزء آن عمود بر مرز با توجه به موارد زیر تعریف کرد:
چگالی جریان را می توان شامل تمام اجزای آن نیز تعریف کرد:
جایی که i l , bnd یک عبارت داده شده برای بردار چگالی جریان است.
چگالی جریان الکترولیت |
نظریه جریان الکترولیت
شرایط مرزی جریان الکترود ، جریان کل را در یک موقعیت معین در الکترولیت بدون تحمیل توزیع چگالی جریان تنظیم می کند. این شرایط یک پتانسیل الکترولیت ثابت را در امتداد مرز داده شده ایجاد می کند که مقدار کل جریان را برآورده می کند. شرایط مرزی انتخاب خوبی در وسط یک سلول با الکترودهای مسطح است، جایی که سطح هم پتانسیل می تواند یک صفحه (یا نزدیک به صفحه در سه بعدی یا خط در دو بعدی) باشد، اما در جایی که توزیع چگالی جریان ناشناخته است.
این ویژگی یک متغیر ناشناخته، پتانسیل الکترولیت،  l ، bnd را در امتداد مرز اضافه می کند. سپس یک معادله اضافی برای جریان کل اضافه می کند که یک انتگرال بر روی مرز است:
l ، bnd را در امتداد مرز اضافه می کند. سپس یک معادله اضافی برای جریان کل اضافه می کند که یک انتگرال بر روی مرز است:
شرط چگالی جریان متوسط همان معادله را تحمیل می کند اما چگالی جریان را در مساحت مرز ضرب می کند تا مقدار جریان کل I n , l را بدست آورد .
نظریه جریان الکترود
جریان الکترود یک متغیر ناشناخته، پتانسیل الکتریکی،  s ، bnd را در امتداد مرز اضافه می کند. سپس یک معادله اضافی برای جریان کل اضافه می کند که یک انتگرال بر روی مرز است:
s ، bnd را در امتداد مرز اضافه می کند. سپس یک معادله اضافی برای جریان کل اضافه می کند که یک انتگرال بر روی مرز است:
جایی که
و σ s نشان دهنده هدایت الکترود و  s پتانسیل الکتریکی است. شرط چگالی جریان متوسط همان معادله را تحمیل میکند اما چگالی جریان را در مساحت مرز ضرب میکند تا مقدار جریان کل، In ,s به دست آید .
s پتانسیل الکتریکی است. شرط چگالی جریان متوسط همان معادله را تحمیل میکند اما چگالی جریان را در مساحت مرز ضرب میکند تا مقدار جریان کل، In ,s به دست آید .
نظریه تقارن
شرط مرزی Symmetry در رابط های توزیع جریان اولیه و توزیع جریان ثانویه با شرایط عایق یکسان است و مطابق معادله زیر بیان می شود.
که در آن i k بردار چگالی جریان را نشان می دهد و k = l ، s به ترتیب شاخصی برای الکترولیت و الکترود است.
شرط مرزی تقارن برای توزیع جریان سوم، رابط نرنست-پلانک یک شرط بدون شار را برای شار مولی گونه ها در یک مرز تحمیل می کند. شرط به صورت زیر بیان می شود:
نظریه چگالی جریان الکترود
چگالی جریان الکترود اعمال شده را می توان به عنوان جزء آن عمود بر مرز با توجه به موارد زیر تعریف کرد:
جایی که
و σ s نشان دهنده هدایت الکترود و  s پتانسیل الکتریکی است.
s پتانسیل الکتریکی است.
چگالی جریان را می توان شامل تمام اجزای آن نیز تعریف کرد:
جایی که i s ، bnd یک عبارت داده شده برای بردار چگالی جریان است.
تئوری قدرت الکترود
شرط مرزی توان الکترود برای مشخص کردن توان کل الکترود یا چگالی توان متوسط الکترود که از یک سلول الکتروشیمیایی در مرز الکترود گرفته شده یا وارد شده است استفاده می شود.
برای شرایط توان کل، پتانسیل الکتریکی مرزی یک الکترود به پتانسیل  s , bnd تنظیم می شود که با شرط توان کل در مرز ∂Ω با توجه به:
s , bnd تنظیم می شود که با شرط توان کل در مرز ∂Ω با توجه به:
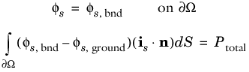
که در  آن s ، زمین پتانسیل زمین سلول است و P کل (W) توانی است که باید کشیده شود.
آن s ، زمین پتانسیل زمین سلول است و P کل (W) توانی است که باید کشیده شود.
برای یک شرایط توان متوسط، P کل با:
که در آن P avg میانگین چگالی توان در مرز است و A منطقه مرزی است.
برای یک سلول گالوانیکی، مانند باتری در حین تخلیه یا پیل سوختی، حداکثر سطح توان وجود دارد که فراتر از آن افزایش بیشتر جریان باعث کاهش توان خروجی به دلیل افزایش تلفات ولتاژ می شود. نتیجه این است که می توان دو راه حل موجود برای تنظیم قدرت یکسان وجود داشت. در این موارد انتخاب مقادیر اولیه راه حل نهایی را تعیین می کند. |
قدرت الکترود |
تئوری غشای تبادل یونی
غشاهای تبادل یونی معمولاً حاوی یک ماتریس پلیمری با تعدادی گروه یونی ثابت هستند.
از آنجایی که این بارها ثابت هستند، نیازی به مدل سازی صریح حمل و نقل این بارها نیست، اما هنگام محاسبه مجموع بارها، که در مجموعه معادلات نرنست-پلانک (با خنثی بودن الکتریکی) یا مجموعه معادلات نرنست-پلانک-پواسون استفاده می شود، نیاز است. برای اضافه کردن این شارژ فضای ثابت.
برای نرنست پلانک با الکتریسیته خنثی بودن، شرط الکتروخنثی خوانده می شود
برای مورد نرنست-پلانک-پواسون، چگالی بار فضایی کل می شود
تئوری مرزی غشاء تبادل یونی
پتانسیل الکتروشیمیایی μi یک گونه باردار شاخص i است
که در آن T (K) دما، R (mol/(JK)) ثابت گاز مولی، a i فعالیت گونه،  پتانسیل الکترولیت، z i بار گونه، و F (C/mol) ثابت فارادی است. .
پتانسیل الکترولیت، z i بار گونه، و F (C/mol) ثابت فارادی است. .
در حالت تعادل پتانسیل های الکتروشیمیایی در هر طرف رابط الکترولیت آزاد – غشاء تبادل یونی برابر است.
تنظیم فعالیت گونه برای برابر غلظت و نشان دادن فاز الکترولیت مایع و فازهای غشای تبادل یونی به ترتیب 1 و 2، پتانسیل Donnan، (V  )، رابطه بین غلظت یک گونه، c i (mol) را توصیف می کند. /m3)، در هر طرف مرز و پتانسیل های الکترولیت:
)، رابطه بین غلظت یک گونه، c i (mol) را توصیف می کند. /m3)، در هر طرف مرز و پتانسیل های الکترولیت:
که ممکن است دوباره تنظیم شود
شار مولی هر گونه در الکترولیت مایع روی سطح مشترک غشا-مایع پیوسته است.
از آنجایی که چگالی جریان کل مجموع شارهای گونهها، برابر بارهای هر گونه است، چگالی جریان I l در جهت عادی n مرز مشترک غشا-مایع نیز پیوسته است:




