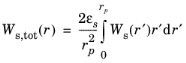رابط باتری لیتیوم یون تعادل جریان در الکترولیت، تعادل جریان در الکترودها، تعادل جرم برای نمک لیتیوم و تعادل جرم لیتیوم در باتریهای لیتیوم یون را تعریف میکند.
الکترولیت در باتریهای مدلسازیشده باید یک الکترولیت باینری ساکن ۱:۱ باشد که حاوی کاتیونهای لیتیوم ( Li + ) و آنیونها ( An- ) باشد.
رابط فیزیک پنج متغیر وابسته را حل می کند:
• |
• |
• | Δs |
• | cs ، غلظت لیتیوم ( Li Θs ) در ذرات الکترود، و |
• | c l ، غلظت نمک الکترولیت. |
در الکترولیت و الکترولیت منفذی دو متغیر l و c l تعریف شده است . با فرض الکتروخنثی بودن، c l هم غلظت Li + و هم غلظت An – را نشان می دهد .
معادلات دامنه در الکترولیت حفظ جریان و تعادل جرم برای نمک بر اساس موارد زیر است:
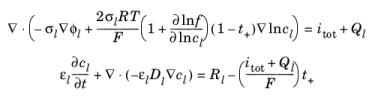
جایی که σl نشان دهنده هدایت الکترولیت، f ضریب فعالیت برای نمک، t + عدد انتقال برای Li + (که عدد انتقال نیز نامیده می شود)، i مجموع همه منابع جریان الکتروشیمیایی، و Ql نشان دهنده یک منبع جریان الکترولیت دلخواه است . . در توازن جرم نمک، εl نشان دهنده کسر حجمی الکترولیت، Dl انتشار نمک الکترولیت، و Rl عبارت منبع کل Li + در الکترولیت است .
در الکترود، چگالی جریان، i s ، به صورت تعریف شده است
که در آن σ رسانایی الکتریکی است .
معادله دامنه برای الکترود، بقای جریان است که به صورت بیان شده است
که در آن Qs یک عبارت منبع جریان دلخواه است .
واکنشهای الکتروشیمیایی در سطح مشترک فیزیک، واکنشهای درج در سطح ذرات کروی کوچک جامد با شعاع r p در الکترودها در نظر گرفته میشوند. واکنش درج به شرح زیر است
که در آن Θ s یک مکان واکنش آزاد و Li Θ s یک مکان واکنش اشغال شده در سطح ذرات جامد است.
غلظت Θ s لازم نیست حل شود زیرا غلظت کل مکان های واکنش، cs , max ثابت فرض می شود، به این معنی که
یکی از پارامترهای مهم برای الکترودهای درج لیتیوم، متغیر حالت بار برای ذرات جامد است که به آن نشان داده شده است . این به عنوان تعریف شده است
پتانسیل های تعادل E 0 واکنش های الکترود درج لیتیوم معمولاً توابع soc هستند .
واکنش الکترود بر روی سطح ذرات رخ می دهد و لیتیوم در ذرات به سطح و از سطح پخش می شود. تعادل جرم لی در ذرات با استفاده از آن شرح داده شده است
که در آن، برای قانون فیک، شار مولی N s به صورت تعریف شده است
که در آن cs غلظت Li در فاز جامد است. این معادله به صورت محلی توسط این رابط فیزیک در یک بعد شبه 1 بعدی، با غلظت فاز جامد در نقاط گره برای گسسته شدن عنصر ذره به عنوان متغیرهای مستقل، حل میشود. گرادیان در مختصات دکارتی، استوانهای یا کروی محاسبه میشود، بسته به این که ذرات بهترتیب بهعنوان پولک، میله یا کره توصیف شوند.
برای مورد انتشار بیکر-وربروژ ( مراجعه 3 )، بردار شار به صورت تعریف شده است.
جایی که
شرایط مرزی به صورت زیر تعریف می شود:
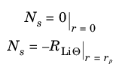
که در آن R Li Θ شار مولی لیتیوم در سطح ذره را نشان می دهد که توسط واکنش های الکتروشیمیایی درج شده ایجاد می شود.
نمادهای استوکیومتری مورد استفاده در رابط فیزیک مطابق با واکنش الکتروشیمیایی عمومی است که در زیر بیان شده است:
که در آن ضرایب استوکیومتری، νi ، مثبت ( ν ox ) برای محصولات و منفی ( ν قرمز ) برای واکنش دهنده ها در واکنش احیا است. از این تعریف، تعداد الکترون ها، n ، در واکنش الکترود را می توان بر اساس محاسبه کرد
جایی که z i نشان دهنده بار گونه i است . با توجه به این روابط، واکنش درج لیتیوم دارای ضرایب استوکیومتری زیر است:
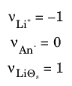
با n = 1 حاصل می شود. این تنظیمات پیش فرض برای واکنش های این رابط فیزیکی هستند. هنگام مدلسازی واکنشهای دیگر، مانند اکسیداسیون آنیون برگشتناپذیر یا رسوب فلز لیتیوم جامد بدون درج، باید از ضرایب دیگری استفاده شود.
در الکترودهای متخلخل، i tot نشاندهنده مجموع تمام سهمهای چگالی جریان انتقال بار بر اساس:
که در آن، A v سطح خاص را نشان می دهد. عبارت منبع در تراز جرم از زیر محاسبه می شود:
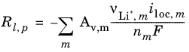
همچنین می توان منابع واکنش اضافی، Rl , src را که به کل منبع گونه کمک می کند، با توجه به موارد زیر مشخص کرد:
در سطح ذرات جامد معادله زیر اعمال می شود:
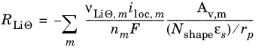
که در آن آخرین فاکتور (معمولاً برابر با 1) یک ضریب پوستهگیری است که تفاوتهای بین سطح ( Av , m ) مورد استفاده برای محاسبه چگالی جریان حجمی و مساحت سطح ذرات در مدل انتشار لیتیوم جامد را محاسبه میکند. شکل N برای مختصات دکارتی 1، برای استوانه ای 2 و برای مختصات کروی 3 است.
اگر ضریب انتشار فاز جامد بسیار بزرگ باشد یا اگر شیب غلظت مکانی در ذره را بتوان نادیده گرفت، تکامل غلظت فاز جامد در زمان را می توان از
منبع مولی R v Θ در الکترودهای مثبت و منفی به صورت زیر ارائه می شود:
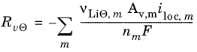
ممکن است یک فیلم مقاومتی (که رابط الکترولیت جامد-الکترولیت SEI نیز نامیده می شود) روی ذرات جامد تشکیل شود که منجر به تلفات پتانسیل اضافی در الکترودها می شود. برای مدلسازی مقاومت فیلم، یک متغیر راهحل اضافی برای تغییر پتانسیل روی فیلم، Δs  ، فیلم ، در رابط فیزیک معرفی میشود. سپس معادله حاکم بر اساس آن است
، فیلم ، در رابط فیزیک معرفی میشود. سپس معادله حاکم بر اساس آن است
که در آن فیلم R (واحد SI: Ω · m 2 ) نشان دهنده مقاومت فیلم تعمیم یافته است. مازاد پتانسیل فعالسازی، ηm ، برای همه واکنشهای الکترود در الکترود، یک سهم پتانسیل اضافی دریافت میکند که نتیجه میدهد .
توزیع اولیه شارژ در سلول باتری
تعداد پارامترها در مدلهای باتری بسیار زیاد است، اما بهویژه تنظیم توزیع بار در سلول (یعنی غلظت گونههای متقابل در هر ماده الکترود) همیشه ساده نیست زیرا اغلب به اطلاعات دقیقتری از ولتاژ و ظرفیت سلول نیاز دارد.
با این حال، می توان توزیع بار اولیه را با در نظر گرفتن اینکه در ابتدا، زمانی که هیچ جریانی روی سلول باتری اعمال نمی شود و منابع قطبش اعمال نمی شود، محاسبه کرد، تنها تفاوت بین پتانسیل تعادل مواد الکترود مثبت و منفی است که دیکته می کند. ولتاژ سلول دو محدودیت را می توان با ظرفیت و ولتاژ سلول باتری به عنوان ورودی برای این محاسبه تنظیم کرد:
• | ظرفیت سلول باتری، سلول Q ، 0 (واحد SI: C)، برابر است با مجموع بار گونه های قابل چرخش، سیکل Q ، در الکترودهای مثبت و منفی (و مواد الکترود متخلخل اضافی در صورت وجود در مدل): |
بار گونه قابل چرخش در یک الکترود یا یک ماده الکترود اضافی به صورت زیر تعریف می شود:
که در آن ε s کسر حجمی الکترود را نشان میدهد و cs ، avg ، چرخه، الکترود میانگین غلظت محلی گونههای قابل چرخش است که به صورت زیر تعریف میشود:
cs ,avg میانگین غلظت گونه است که در ابتدا، زمانی که هیچ گرادیان غلظتی در ذرات الکترود وجود ندارد، برابر با غلظت سطح ذرات الکترود، cs , surf است . soc min حداقل میزان بار مجاز در مواد الکترود است. مقدار شارژ گونه های قابل چرخش مواد الکترود اضافی نیز به طور مشابه محاسبه می شود.
• | پتانسیل الکترود در هر الکترود ثابت است و اختلاف پتانسیل الکترود مثبت و منفی برابر با ولتاژ سلول است: |
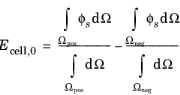
در ابتدا، زمانی که قطبش در سلول وجود ندارد، بیان برابر است با تفاوت در پتانسیل مدار باز مواد الکترود، Eq :
ولتاژ سلول به پتانسیل مدار باز مواد الکترود محدود می شود و ولتاژ سلول باید در محدوده زیر تنظیم شود:
که در آن زیرنویس max و min از حالت شارژ الکترود نشان دهنده حداکثر و حداقل مقدار مجاز گونه های درونی بر حسب حالت بار در مواد الکترود است.
برای هر ماده الکترود اضافی، غلظت درهم محدود شده است تا برآورده شود
از طرف دیگر، محدودیتهای بالقوه را میتوان جایگزین کرد تا به جای آن حالت شارژ اولیه سلول را محدود کند:
• | وضعیت شارژ سلول، سلول سوسیال ، 0 (بدون ابعاد)، ظرفیت سلول باتری را به شارژ گونه های قابل چرخش در هر الکترود مرتبط می کند: |
حالت شارژ سلول بین 0 تا 1 است. حالت شارژ 0 نشان می دهد که سلول کاملاً تخلیه شده است و اگر 1 باشد سلول کاملاً شارژ شده است.
متعادل کردن الکترودها
تعادل الکترودها در سلول به این معنی است که مقدار ماده فعال الکترود در هر الکترود پس از ظرفیت سلول باتری طراحی می شود. به عبارت دیگر، ظرفیت گونههای چرخهپذیر را میتوان به طور کامل در الکترود مثبت یا منفی بدون داشتن مواد اضافی استفاده نشده و برای حفظ غلظت گونههای درونگیر در پنجره وضعیت شارژ مشخص شده میزبانی کرد. برای باتری ها این امر برای به حداکثر رساندن چگالی انرژی و طول عمر و گاهی اوقات به دلایل ایمنی از اهمیت بالایی برخوردار است.
رابط باتری می تواند بخش های حجمی الکترود را تامین کند که الکترودها را متعادل می کند. اینها با اتصال مقدار ماده میزبان فعال – یعنی حداکثر مقدار گونههای قابل چرخش در الکترود – به ظرفیت اولیه سلول محاسبه میشوند. در اینجا، ماده میزبان فعال در الکترود مثبت برابر با ظرفیت سلول تنظیم می شود. در برخی از شیمی باتری ها، به عنوان مثال باتری های لیتیوم یون، مقدار ماده میزبان در هر دو الکترود منحرف می شود. به خصوص، الکترودهای مبتنی بر کربن منفی اغلب در مقایسه با الکترود مثبت بیش از حد تنظیم میشوند تا تلفات برگشتناپذیر در سلول را در حین کار ایجاد کنند. گونه های قابل چرخش در برخی موارد می توانند مستقیماً پس از مونتاژ سلولی از بین بروند. بنابراین روابط زیر اعمال می شود:
که در آن میزبان Q (واحد SI: C) مقدار ماده میزبان فعال، چرخه f ، از دست دادن کسری گونههای چرخهپذیر، و f میزبان، منفی، خارج از مازاد کسری ماده میزبان فعال منفی است.
برای محاسبه کسر حجمی الکترود، این واقعیت که مقدار ماده میزبان فعال را می توان از معادله زیر محاسبه کرد، باید در نظر گرفته شود:
جایی که Δ soc پنجره حالت شارژ مجاز ماده الکترود است.
بنابراین بیان کسر حجمی الکترود در هر الکترود به صورت زیر است:
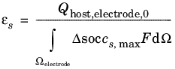
از کسر حجمی الکترود نشان داده شده است که ظرفیت سلول باتری باید با دقت انتخاب شود، زیرا ظرفیت توسط مواد و اندازه الکترود محدود می شود. ظرفیت هرگز نباید طوری تنظیم شود که کسر حجمی الکترود بزرگتر از 1 باشد.
توجه داشته باشید که بالانس الکترود که در بالا توضیح داده شد، مواد اضافی الکترود را در نظر نمی گیرد.
تنش و کرنش در ذرات درهم
ماده میزبان الکترود می تواند در طول شارژ و دشارژ دستخوش تغییرات حجمی قابل توجهی شود. اگر شیب غلظت در ذرات الکترود وجود داشته باشد که منجر به تغییر شکل الاستیک ناهمگن می شود، این باعث ایجاد تنش می شود.
از آنجایی که انتشار اتمی در جامدات فرآیندی بسیار کندتر از تغییر شکل الاستیک است، تعادل مکانیکی بسیار سریعتر از انتشار برقرار می شود. از این رو، تعادل مکانیکی را می توان به عنوان یک مشکل تعادل ایستا در نظر گرفت. در تجزیه و تحلیل زیر، ذرات الکترود (کره ها یا استوانه ها) به عنوان جامدات الاستیک خطی همسانگرد فرض می شوند.
تغییر نسبی در حجم δV / V 0 معمولاً به غلظت فاز جامد cs ( یا متغیر حالت شارژ soc ) بستگی دارد. توجه داشته باشید که cs در یک بعد اضافی 1 بعدی با استفاده از سیستم مختصات کروی یا استوانه ای (به ترتیب برای کره یا استوانه)، همانطور که در بالا توضیح داده شد، حل می شود . در معادلات ارائه شده در زیر ، تغییر حجم نسبی تابعی از غلظت Δ V / V 0 = f vol ( cs ( r )) در نظر گرفته میشود .
نوع ذرات: کره
روابط بین تنش، σ( r ) (واحد SI: Pa)، و کرنش، ε( r ) (واحد SI: 1)، که در سیستم مختصات کروی برای اجزای شعاعی و مماسی بیان شده است (با توجه به آن  )
)
که در آن E (واحد SI: Pa) مدول یانگ و ν (واحد SI:1) نسبت پواسون است. فرض بر این است که این خواص کشسان مستقل از غلظت هستند.
عبارات تنش های شعاعی و مماسی در یک ذره کروی با شعاع rp که شرط مرزی σr ( rp ) = 0 را برآورده می کند و در r = 0 محدود می ماند ، می تواند با حل معادله تعادل مکانیکی استاتیک به صورت زیر به دست آید. در غیاب نیروی بدن:
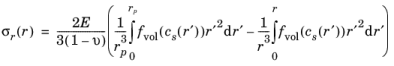
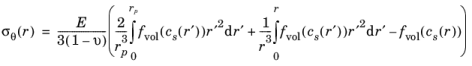
که در آن دو انتگرال به ترتیب سهمی را نشان میدهند، یکی از یک انتگرال در کل حجم ذره کروی و دیگری با یک انتگرال در یک حجم کروی به شعاع r درون ذره داده میشود. توجه داشته باشید که جزء مماسی علاوه بر این شامل یک عبارت محلی است که توسط آخرین عبارت در عبارت ارائه شده است.
تنش هیدرواستاتیک σh ( r ) (واحد SI: Pa) (یا تنش متوسط) با
تنش فون میزس σ v ( r ) (واحد SI: Pa) داده شده توسط
به دلیل تقارن کروی، یک تنش برشی اصلی صفر و دو تن دیگر هر دو برابر هستند  .
.
چگالی انرژی کرنش Ws ( r ) (واحد SI: J/m 3 ) انباشته شده در نتیجه تغییر شکل الاستیک برای کره تغییر شکل همسانگرد به صورت داده شده است .
چگالی انرژی کرنش الاستیک کل ذخیره شده در ماده الکترود میزبان Ws ,tot ( r ) (واحد SI: J/m 3 ) که نیروی محرکه شکست را فراهم می کند، به دست می آید:
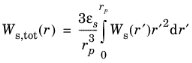
که در آن ε s کسر حجمی الکترود در ماده میزبان است.
نوع ذرات: سیلندر
روابط بین تنش، σ( r ) و کرنش ε( r ) که در سیستم مختصات استوانه ای برای مولفه های شعاعی، مماسی و محوری بیان می شود به شرح زیر است:
عبارات تنش های ناشی از انتشار شعاعی، مماسی و محوری برای یک ذره استوانه ای همسانگرد عرضی با شعاع r p عبارتند از:
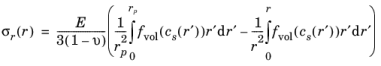
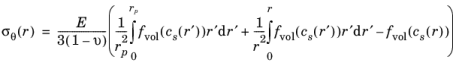

تنش هیدرواستاتیک σ h ( r ) توسط:
تنش فون میزس σ v ( r ) توسط
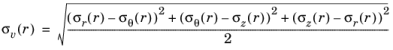
چگالی انرژی کرنش Ws ( r ) انباشته شده در نتیجه تغییر شکل الاستیک برای استوانه تغییر شکل همسانگرد به صورت داده شده است .
کل چگالی انرژی کرنش الاستیک ذخیره شده در ماده الکترود میزبان Ws ,tot ( r ) به صورت