هنگامی که یک موج صوتی با فرکانس زاویه ای معین ω به یک موجبر یا یک مجرا وارد می شود، تنها مجموعه محدودی از اشکال یا حالت ها برای میدان فشار عرضی می تواند در فواصل طولانی در داخل سازه منتشر شود. هر چه فرکانس بیشتر باشد، تعداد حالت های پایدار بیشتر است.
به عنوان مثال، یک مجرای مستقیم یکنواخت که محور آن در جهت z است را در نظر بگیرید . میدان صوتی در چنین مجرای را می توان به صورت مجموع فرم نوشت
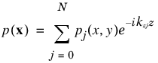
ثابت kzj عدد موج محوری j امین حالت عرضی انتشار است ، pj ( x , y ) . این حالتهای عرضی و اعداد موج محوری مرتبط با آنها راهحلهایی برای یک مسئله ارزش ویژه تعریفشده بر روی مقطع مجرا هستند. قابلیت های تجزیه و تحلیل حالت در The Pressure Acoustics، Boundary Mode Interface حل چنین مسائل ارزش ویژه را ممکن می سازد. رابط فیزیک برای هندسههای سهبعدی دکارتی و دوبعدی متقارن محوری موجود است و حالتهای ویژه عرضی را برای فشار صوتی p و ثابتهای انتشار مرتبط kz حل میکند . اینمطالعه تحلیل حالت به طور خلاصه مورد بحث قرار گرفته است.
مطالعه تحلیل حالت
حل کننده مقدار ویژه تعداد مشخصی از راه حل های { p j , λ j } را برای معادله محاسبه می کند.
(2-22)
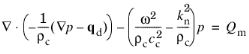
بر روی یک مرز دو بعدی از دامنه مدل سازی (در سه بعدی) یا در خود دامنه دو بعدی، با λ = – ik n به عنوان مقدار ویژه تعریف شده است. در این معادله p فشار درون صفحه، ρc چگالی، cc سرعت صوت، ω فرکانس زاویه ای و kn ثابت انتشار در جهت نرمال به سطح است، در این زمینه . به آن عدد موج خارج از صفحه نیز گفته می شود.
عدد موج خارج از صفحه k n نشان داده می شود و در جهت عادی به سطح دو بعدی است که معادله 2-22 روی آن است . همانطور که برای مطالعه تجزیه و تحلیل حالت در حوزه فرکانس، جهت انتشار لزوماً نباید برای هندسه های سه بعدی نسبت به محور z نرمال باشد . |
متغیرهای ویژه پس پردازش برای رابط آکوستیک فشار، حالت مرزی وجود دارد. آنها در آکوستیک فشار، متغیرهای حالت مرزی توضیح داده شده اند . |
توجه داشته باشید که معادله فوق با معادله زمان هارمونیک برای آکوستیک فشار یکسان است، با این تفاوت که k n به عنوان یک مقدار ویژه تفسیر می شود نه به عنوان یک پارامتر.
برای هندسه های متقارن محور، معادله مقدار ویژه مربوطه برای حل حالت های فشار شعاعی و مقادیر ویژه λ است.
در اینجا m ، عدد حالت آزیموتال ، یک پارامتر با مقدار صحیح است. معادله در بازه r 1 < r < r 2 تعریف شده است . مقدار ویژه λ بر حسب عدد موج محوری kz از طریق معادله λ = – ik z تعریف می شود .




