The multicomponent Fick diffusivities, , are needed to solve Equation 3-50. The diffusivities are symmetric

and are related to the multicomponent Maxwell–Stefan diffusivities, Dik, through the following relation (Ref. 2)

where (adjBi)jk is the jkth component of the adjoint of the matrix Bi.

For low-density gas mixtures, the multicomponent Maxwell–Stefan diffusivities, Dij, can be replaced with the binary diffusivities for the species pairs that are present.

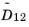
Solving for Equation 3-51 leads to a number of algebraic expressions for each of the components in the multicomponent Fick diffusivity matrix. For two- and three-component systems, these are implemented and solved directly by COMSOL Multiphysics. For instance, the component in a ternary system is given by:

For four components or more, COMSOL Multiphysics obtains the multicomponent Fick diffusivities numerically through matrix inversion derived from the matrix properties defined in Ref. 2. The program starts with the multicomponent Maxwell–Stefan diffusivity matrix Dik to compute the multicomponent Fick diffusivity matrix, , using the following equation:

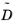
where ij are indices in the matrices and N, and ranges from 1 to the number of species, Q.

The elements of the matrix N in Equation 3-52 are defined as

where P−1 is the inverse of a matrix P defined as

The term g in Equation 3-52 is a scalar value that provides numerical stability and should be of the same order of magnitude as the multicomponent Maxwell–Stefan diffusion coefficients. The physics interface therefore defines q as the sum of the multicomponent Maxwell–Stefan diffusion coefficients:

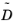
Because the multicomponent Fick diffusivity matrix is symmetric, it is sufficient to apply Equation 3-53 to the upper triangle elements of . The remaining elements are obtained by swapping the indices in the matrix.
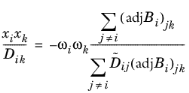