مدل انتشار آکوستیک بر این فرض استوار است که حجمها (اتاقهای) مورد مطالعه حاوی پراکندههایی هستند که به طور یکنواخت میدان صوتی را پراکنده میکنند و میدان صوتی منتشر است (تعداد زیاد بازتاب). با استفاده از انتشار نور در یک محیط پراکندگی به عنوان یک قیاس، می توان معادله انتشار برای چگالی انرژی صدا w = w ( x , t ) بیان کرد (واحد SI: J/m 3 ). معادله انتشار جریان انرژی از مناطق پر انرژی به مناطق کم انرژی را توصیف می کند. جزئیات بیشتر در مورد معادلات مدل و شرایط مرزی در مقالات شیانگ و دیگران یافت می شود (رجوع کنید به شماره 3 ، شماره 7 و مرجع 8 مراجعه کنید.) و در مقالات Billon، Valeau، و بیشتر (رجوع کنید به مرجع 5 ، مرجع 6 ، مرجع 11 ، و مرجع 15 ).
معادلات دامنه
معادله انتشار دامنه برای چگالی انرژی صوت w = w ( x , t ) با
که در آن بردار شار انرژی محلی J (واحد SI: J/m 2 /s = W/m 2 ) به روش معمول تعریف می شود، به عنوان
ضریب انتشار کل D t = D = λ c / 3 (واحد SI: m 2 / s)، λ میانگین مسیر آزاد (واحد SI: m)، c سرعت صوت (واحد SI: m/s) است. ) و m a ضریب جذب حجمی هوا است (واحد SI: 1/m). ضریب جذب حجمی (یا ضریب میرایی) نباید با ضریب جذب انرژی α که در شرایط مرزی بدون بعد استفاده می شود، اشتباه گرفته شود. عبارت منبع q نشان دهنده منبع صوتی مکانی است (واحد SI: J/m 3 /s = W/m 3 ). عبارت cm a w برای جذب حجمی در هوا (اتلاف) است. توجه داشته باشید که در مدلهای خاصی، عبارت cm a w جذب کل در مرزها را به معنای «میانگین» محاسبه میکند (فقط با استفاده از شرایط مرزی شار)، این رویکرد در اینجا استفاده نمیشود.
در رابط، m a می تواند به عنوان ورودی کاربر داده شود یا می توان آن را به عنوان ضریب “کلاسیک چسبناک و جذب حرارتی (حجمی)” تعریف کرد (مانند آکوستیک فشار) که توسط
ضریب جذب یا روی باند یکپارچه می شود یا در فرکانس مشخصی داده می شود. جذب حجمی فقط برای دامنه ها/اتاق های بسیار بزرگ مهم است. علاوه بر این فرض می شود که m a λ << 1 به طوری که ضریب انتشار بدون تغییر باقی می ماند.
میانگین مسیر آزاد λ فاصله ای است که یک ذره صوت به طور متوسط بین بازتاب ها طی می کند.  با میانگین فرکانس بازتاب λ = c / مرتبط است
با میانگین فرکانس بازتاب λ = c / مرتبط است  . میانگین مسیر آزاد یکی از ویژگی های هر اتاق است و برای یک اتاق مکعبی معمولی می توان آن را با (قرارداد معمول) محاسبه کرد.
. میانگین مسیر آزاد یکی از ویژگی های هر اتاق است و برای یک اتاق مکعبی معمولی می توان آن را با (قرارداد معمول) محاسبه کرد.
که در آن V حجم اتاق و S کل سطح اتاق است (رجوع کنید به شماره 18 ). میانگین مسیر آزاد برای هر اتاق تعریف می شود زیرا به هندسه و شکل اتاق بستگی دارد. برای اتاقهای طولانی مانند راهروها، Visentin (رجوع کنید به شماره 13 و 14 مراجعه کنید) پیشنهاد میکند از تعریف دیگری از میانگین مسیر آزاد استفاده شود.
به طور کلی، میانگین مسیر آزاد برای اشکال مختلف اتاق متفاوت است. وارد کردن یک مسیر آزاد میانگین تعریف شده توسط کاربر بر اساس اندازهگیریهای نمونه نیز امکانپذیر است (رجوع کنید به شماره 1 ، شماره 2 ، و مرجع 17 ).
اتاق های مجهز/مناطق دارای موانع (صندلی، ماشین آلات و غیره)
در مناطق دارای اتصالات، مانند مبلمان یا سایر جاذبها، پراکندهها با چگالی عددی nf ( واحد SI : 1/m 3 )، میانگین مقطع Qf (واحد SI: m2 ) و جذب آنها مدلسازی میشوند. ضریب α f (بدون بعد). برای دامنه دارای پراکنده، مسیر آزاد متوسط می شود
تعریف ثابت انتشار برازش
با وجود این تعاریف، معادله انتشار حاکم را می توان برای در نظر گرفتن برازش اصلاح کرد (به عنوان مثال، رفر. 15 را ببینید ) .
اعتبار
محدودیت زمانی که پس از آن مدل انتشار صوتی منجر به نتایج صحیح می شود توسط بسیاری از نویسندگان مورد بحث قرار گرفته است. به عنوان مثال Ref. 6 ، ر. 12 یا Ref. 15 . آنها پیشنهاد می کنند که محدودیت یک میانگین زمان آزاد λ / cمی توان برای معادله انتشار در نظر گرفت که معنای فیزیکی داشته باشد. قبل از این زمان، احتمال بالای برخورد نکردن ذرات به یک پراکنده/سطح و در عین حال منجر به نتایج نامعتبر می شود. به طور معمول، این نوع مدل ها فقط در فرکانس های بالاتر از فرکانس شرودر اعمال می شوند. این یک معیار “قاعده سرانگشتی” خوب است – در چندین نشریه دیده شده است که نتایج با اندازه گیری ها در فرکانس های پایین تر مطابقت دارند. در زیر فرکانس شرودر، حالت های ویژه اتاق مهم هستند و می توانند با استفاده از آکوستیک فشار مدل شوند.
منابع
عبارت منبع q ( x , t ) (واحد SI چگالی توان J/m 3 /s = W/m 3 ) را می توان به عنوان منبع نقطه ای یا منبع حجمی تعریف کرد.
• | منبع نقطه ای واقع در x s از نوع q ( x , t ) = P ( t ) δ ( x – x s ) هستند که در آن P توان منبع (واحد SI: W) است. |
• | منابع حجم/دامنه حجم Vs که توان Q را ساطع میکنند (واحد SI: W) که چگالی توان Q / Vs را ایجاد میکند . |
• | یک منبع ضربه در یک مدل گذرا معمولاً به عنوان مقدار اولیه w ( x ,0) در یک حوزه کوچک معین (ثابت در فضا) مدلسازی میشود. منبع (مقدار اولیه) همچنین می تواند به شکل گاوسی در فضا باشد، در اینجا یک دامنه بزرگتر. |
شرایط مرزی
دیوار (با ویژگی های جذب متفاوت)
در دیوارها، از یک شرایط مرزی مختلط برای محاسبه تلفات جذب استفاده می شود (سطح نرمال n به سمت بیرون به حجم Ω است )
که در آن h ضریب مبادله است. مدل های مختلفی برای این ضریب وجود دارد که توسط Xiang و دیگران ارائه شده است (رجوع کنید به مرجع 3 و مرجع 4 ). ضریب تعویض نوع سابین می باشد
این عبارت برای سطوحی که ضریب جذب کمتر از 0.2 است معتبر است. مدل نوع آیرینگ توسط
این مدل برای ضرایب جذب نزدیک به 1 مناسب نیست. در نهایت، مدل (اصلاح شده) توسط Jing و Xiang وجود دارد (رجوع کنید به شماره 4 ) .
در این مدل، شرایط مرزی از نظر تئوری زمین است و می تواند جذب بالا را برای بخش کوچکی از سطوح مدل کند. علاوه بر این، مدل معادله انتشار ذاتاً فرض میکند که جذب کلی در اتاقهای تحت آزمایش نباید “بالا” باشد.
پیش از میلاد داخلی (اتصال بین اتاقها/حجمها)
در مرزهای داخلی بین اتاقها (دیوارهای نازک، درها، کورهها، پانلهای نازک و غیره) ممکن است افت انتقال (TL) مرتبط باشد. تلفات انتقال مربوط به ضریب انتقال τ مرز به عنوان است
این منجر به شرایطی می شود که در آن میدان w در سراسر مرز ناپیوسته است (یک شکاف). با استفاده از قراردادهای معمول بالا/پایین شرایط، از جمله جذب احتمالی. TL برای یک دهانه معمولاً برای مرزی که دهانه در آن قرار دارد داده می شود. یعنی انتقال ترکیبی و جذب روی یک مرز آغشته می شود.
با اشاره به سطح نرمال از دامنه ها، شار در سمت پایین سطح/دیوار (از جمله جذب) است.
در سمت بالا سطح/دیوار (شامل جذب) شار کل است
ضریب انتقال به دلیل رابطه متقابل از هر دو طرف یکسان است. این منجر به شرایط ترکیبی می شود
شرط “اتصال اتاق” شارهای مربوط به TL را اضافه می کند. همچنین توجه داشته باشید که شرایط نوع τcw /4 احتمالاً باید برای TL کوچک اصلاح شود زیرا τ سپس بزرگتر از 0.2 (در حدود 7 دسی بل) می شود. گزینه ای برای تحمیل تداوم با محدود کردن وجود دارد
که اساساً مربوط به از دست دادن انتقال صفر است.
شرایط مرزی ورودی و خروجی
برخی از شرایط مرزی کلی که یک جریان ورودی یا خروجی کل انرژی را تعریف میکنند، اضافه میشوند
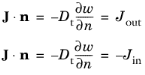
پس پردازش متغیرها/عبارات
فشار مربع (معتبر برای مقادیر و حجم های میانگین مکانی که در مقایسه با طول موج بزرگ هستند اما در مقایسه با مسیر آزاد متوسط کوچک هستند):
حل معادله انرژی (با یک منبع ضربه) پاسخ ضربه اتاق انرژی را به دست می دهد (به استثنای صدای مستقیم، زیرا میدان صوتی منتشر فرض می شود). همچنین به عنوان تابع انرژی-زمان (ETF) یا منحنی انرژی-زمان (ETC) شناخته می شود. پاسخ SPL توسط
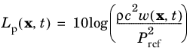
این به طور کلی SPL محلی برای هر منبع است. برای یک مدل حالت پایدار، این توزیع فضایی SPL L p ( x ) است.
واپاشی انرژی صوتی حالت پایدار d ( x , t ) را می توان از روی یک پاسخ تکانه انرژی با استفاده از به اصطلاح ادغام شرودر محاسبه کرد. این مربوط به پیدا کردن حالت پایدار (با استفاده از یک حل کننده ثابت) و سپس استفاده از این راه حل به عنوان شرایط اولیه (منبع خاموش) در یک مدل وابسته به زمان است. همان پاسخ را می توان با استفاده از ادغام شرودر یک مدل پاسخ ضربه ای محاسبه کرد
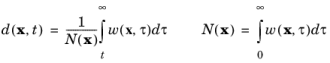
این ادغام را می توان در پس پردازش COMSOL Multiphysics با استفاده از عملگر داخلی ()timeint راه اندازی کرد .
یک متغیر برای ارزیابی پسینی از برآورده شدن فرض میدان پراکنده با (نام “هنجار ارزیابی میدان پراکنده پسینی” در لیست پس پردازش) ارائه می شود.
اگر این متغیر کوچک باشد، فرض انتشار آکوستیک برآورده می شود. متغیر دیگری که می توان آن را ارزیابی کرد، فرکانس شرودر است که در بالا ذکر شد.
انواع مختلف مطالعه
گذرا
یک شبیهسازی گذرا برای مدلسازی پاسخ تکانه انرژی (پاسخ به منبعی از نوع E 0 λ ( t )، که معمولاً با یک تابع پله از زمان پیراهن تقریب میشود) یک اتاق یا پاسخ فروپاشی انرژی در حالت پایدار استفاده میشود. پوسیدگی از محلول حالت پایدار). در یک اتاق یک نفره پاسخ در تمام نقاط (به جز یک تاخیر زمانی کوچک) یکسان خواهد بود. این به تخمین زمانهای طنین (RT) یکسان منجر میشود. علاقه مدل گذرا زمانی مشهودتر است که چندین اتاق جفت شوند. در اینجا چندین مقیاس زمانی به دلیل تعامل بین اتاق ها وجود دارد و اینها را می توان در یک پاسخ تکانه انرژی گذرا مشاهده کرد.
حالت پایدار
مدل حالت پایدار برای یافتن توزیع فضایی SPL در داخل یک اتاق یا مجموعه ای از اتاق ها و حجم ها زمانی که در معرض یک منبع نویز ثابت قرار دارند استفاده می شود. این می تواند صدای موتور یا صدای تولید شده توسط ماشین آلات دیگر باشد.
مقدار خاص
تجزیه و تحلیل ارزش ویژه از معادله گذرا منجر به تمام “توابع پایه” مسئله می شود. یعنی حالت هایی که در فضا تغییر شکل نمی دهند بلکه فقط در زمان با مقیاس زمانی نمایی داده شده توسط مقدار ویژه تحلیل می روند. از نوع هستند
که در آن λ i مقدار ویژه i:ام و w i حالت مرتبط است. مقادیر ویژه اندازه گیری مستقیم زمان طنین (RT) اتاق های مختلف است. T 60 به عنوان مثال به سادگی توسط داده شده است
که در آن آخرین معادله عبارت کلاسیک است. ارزیابی مقادیر ویژه اندازه گیری آسانی از شیب توابع انرژی-زمان (ETFs) ارائه می دهد و می تواند با یک مدل گذرا ترکیب شود تا تصویر کاملی از طنین در حجم های مختلف (اتاق ها) و رفتار همراه آنها ارائه شود. هنگام انجام یک مطالعه مقدار ویژه، متغیر ade.T60 زمان طنین مرتبط با مقدار ویژه داده شده را نشان می دهد. نمودار حالتهای چگالی انرژی صدا را بررسی کنید تا مشخص کنید زمان طنین به کدام اتاق مربوط میشود.




