به طور کلی، حرکت یک سیال نیوتنی تراکم پذیر چسبناک، از جمله معادله انرژی، توسط مجموعه معادلات فهرست شده در معادله 6-4 زیر کنترل می شود.
(6-4)
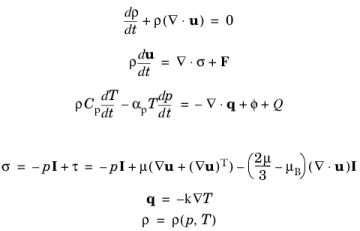
که در آن متغیرهای وابسته فشار p ، سرعت u ، دما T و چگالی ρ هستند . سه معادله اول به ترتیب معادله تداوم، معادله تکانه (معادله ناویر-استوکس) و معادله انرژی هستند. سه معادله آخر معادلات سازنده هستند. آنها تانسور تنش کل σ و تانسور تنش ویسکوز τ را از طریق بیان استوکس، قانون هدایت حرارت فوریه و یک معادله حالت تعریف می کنند. به عنوان مثال Ref. 1 تا 7 برای جزئیات بیشتر
مشتقات زمان مادی (یا مشتقات کل) d / dt به شرح زیر است که بر اساس
که در آن A یک متغیر ساختگی است. معادله حالت مقادیر محلی فشار، چگالی و دما را به هم مرتبط می کند و بنابراین یک معادله جبری یا ODE است نه PDE. شکل رایج معادلات حالت دانستن چگالی به عنوان تابعی از فشار و دما، ρ = ρ( p , T ) است. در ادامه فرض بر این است که معادله حالت این شکل را دارد.
خواص اساسی سیال ویسکوزیته دینامیکی μ و هدایت حرارتی k است . ضریب μ B ویسکوزیته حجیم (یا دوم) است و تلفات ناشی از تراکم پذیری (انبساط و انقباض سیال) را توصیف می کند، در حالی که μ تلفات ناشی از اصطکاک برشی را توصیف می کند. ویسکوزیته توده ای را می توان در برخی موارد برای مدلسازی یک انحراف مشاهده شده تجربی از فرض استوکس استفاده کرد، اما معمولاً در مقایسه با μ ناچیز است مگر اینکه حرکت غیر چرخشی باشد. رجوع کنید به رفر. 3 و ر. 4 . این سه ویژگی ثابت یا حداکثر ضعیف وابسته به دما هستند. گرمای ویژه در فشار ثابت C p(در واحد جرم) و ضریب (ایزوباریک) انبساط حجمی حرارتی α p (گاهی اوقات α 0 نشان داده می شود )،
هر دو احتمالاً تابع فشار و دما هستند.
در معادله انرژی
تابع اتلاف ویسکوز است – یعنی انقباض اسکالر تانسور تنش ویسکوز τ با نرخ تانسور کرنش S . هر دو تانسور به عنوان تابعی از یک بردار سرعت دیده می شوند. اگر سرعت متوسط صفر باشد، این عبارت در خطیسازی زیر ناپدید میشود، زیرا در گرادیانهای سرعت از مرتبه دوم همگن است. در غیر این صورت، به عنوان یک منبع یا سینک نوسانی عمل می کند (این اصطلاح در رابط های خطی کامل Navier-Stokes گنجانده شده است). در سمت راست معادله 6-4 ، F و Q به ترتیب یک نیروی حجمی و یک منبع گرما هستند.




