ماژول آکوستیک عملکردی برای ارزیابی میدان فشار آکوستیک در ناحیه میدان خارجی مدل (خارج از حوزه محاسباتی) دارد. این بخش تعاریف مربوطه و پیشینه ریاضی و همچنین توصیه های کلی برای تجزیه و تحلیل میدان بیرونی را ارائه می دهد. جزئیات در مورد نحوه استفاده از عملکرد میدان بیرونی در محاسبه میدان خارجی و در بخش مدلسازی ارزیابی میدان صوتی در قسمت بیرونی: میدان نزدیک و دور توضیح داده شده است .
بازنمایی انتگرال هلمهولتز-کیرشهوف
در بسیاری از موارد، حل معادله هلمهولتز آکوستیک در همه جای حوزه ای که نتایج درخواست شده است، نه عملی است و نه ضروری. برای محیط های همگن، محلول در هر جایی خارج از یک سطح بسته که شامل همه منابع و پراکنده ها است، می تواند به عنوان یک انتگرال مرزی بر حسب مقادیر ارزیابی شده روی سطح نوشته شود. برای ارزیابی این انتگرال هلمهولتز-کیرشهوف ، لازم است هر دو مقدار دیریکله و نویمان را در سطح بدانیم. در مورد آکوستیک، این بدان معنی است که اگر فشار و مشتق نرمال آن (که مربوط به سرعت نرمال است) در یک سطح بسته شناخته شود، میدان صوتی را می توان در هر نقطه از خارج محاسبه کرد.
به طور کلی، حل p معادله هلمهولتز
در حوزه همگن بیرونی یک سطح بسته، S را می توان به صراحت بر حسب مقادیر p و مشتق نرمال آن در S بیان کرد :
در اینجا بردار مختصات r S را پارامتر می کند . بردار واحد n نرمال بیرونی به حوزه بینهایت بیرونی است. بنابراین، n به دامنه ای که S محصور می کند اشاره می کند . تابع G ( R , r ) یک تابع گرین راضی کننده است
این اساسا به این معنی است که تابع گرین که به عنوان تابعی از r در نظر گرفته می شود ، یک موج سیار خروجی است که توسط یک منبع ساده در R برانگیخته می شود . بنابراین، در سه بعدی، تابع سبز به این صورت است:
در دوبعدی، تابع گرین به جای تابع نمایی شامل یک تابع Hankel است:
با وارد کردن تابع 3D Green در فرمول نمایش کلی به دست می آید:
(2-23)
در حالی که در دو بعدی، تابع Hankel به یک عبارت کمی متفاوت منجر می شود:
(2-24)
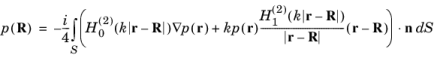
برای هندسه های متقارن محوری، انتگرال کامل سه بعدی باید ارزیابی شود. ماژول آکوستیک از یک ربع عددی تطبیقی در جهت آزیموتال بر روی یک هندسه گردان ساختگی علاوه بر ربع استاندارد مبتنی بر مش در صفحه rz استفاده می کند .
پیش فرض در ویژگی محاسبه میدان خارجی ارزیابی انتگرال هلمهولتز-کیرشهوف کامل است که در معادله 2-23 و معادله 2-24 ارائه شده است .
حد میدان دور
انتگرال کامل Helmholtz-Kirchhoff فشار را در هر نقطه در یک فاصله محدود از سطح منبع می دهد، اما ادغام عددی تمایل به از دست دادن دقت در فواصل بسیار زیاد دارد. در عین حال، در برخی از کاربردها، کمیت مورد نظر الگوی تابش میدان دور است که می تواند به عنوان حد r تعریف شود | p | وقتی r در یک جهت معین به بی نهایت می رود.
در نظر گرفتن حد معادله 2-23 وقتی | R | به سمت بی نهایت می رود و با نادیده گرفتن ضریب فاز به سرعت در حال نوسان، میدان دور، p far به صورت
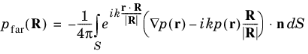
مقدار مربوطه | p far | به جای p far ، زیرا فاز دومی تعریف نشده است. به همین دلیل، فقط جهت R مهم است، نه بزرگی آن. |
از آنجا که توابع هانکل به صورت مجانبی به یک نمایی نزدیک می شود، انتگرال دو بعدی محدود کننده به طور قابل توجهی شبیه به حالت سه بعدی است:
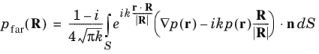
برای هندسه های متقارن محوری، انتگرال آزیموتال حالت سه بعدی محدود کننده را می توان به صورت تحلیلی مدیریت کرد، که منجر به یک بیان نسبتاً پیچیده می شود، اما از ربع عددی مورد نیاز در حالت کلی اجتناب می کند. برای عدد حالت آزیموتال صفر m = 0، عبارت به صورت زیر است:
(2-25)
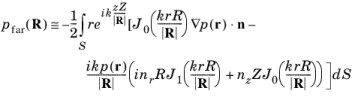
در این انتگرال، r و z اجزای شعاعی و محوری r هستند ، در حالی که R و Z اجزای شعاعی و محوری R هستند .
برای ارزیابی فشار در حد میدان دور با توجه به معادلات این بخش، گزینه Type of integral را روی گزینه Far-field integral approximation for r → ∞ در قسمت Exterior Field Calculation در پنجره Settings برای ویژگی تنظیم کنید. محاسبه میدان خارجی را ببینید .
عنصر الکرنل
این انتگرال ها را می توان به عنوان متغیرهای جفت ادغام در COMSOL Multiphysics پیاده سازی کرد. با این حال، چنین رویکردی بسیار ناکارآمد است زیرا در این صورت ساختار ساده هسته های یکپارچه سازی نمی تواند مورد سوء استفاده قرار گیرد. بنابراین، در ماژول آکوستیک، انتگرالهای کانولوشن از این نوع در کدهای بهینهسازی شده ارزیابی میشوند که تمام جزئیات را از کاربر پنهان میکند.




