نسخه های فعلی
2
زیرنوع از
GeomCurve
زمینه های
ENTITY/OBJECT | متغیر | شرح |
عدد صحیح | نسخه. | |
عدد صحیح | د | بعد فضایی |
بولی | اگر منحنی گویا باشد 1، اگر منحنی چند جمله ای (غیر منطقی) باشد 0. | |
بولی | اگر منحنی تناوبی باشد 1، اگر تناوبی نباشد 0. | |
عدد صحیح | پ | درجه. |
عدد صحیح | متر | وکتور طول گره. |
دوبرابر[m] | U | وکتور گره. |
double[n][k] | Pw | نقاط کنترل منحنی تعداد نقاط کنترل، n، با n = m – p – 1 به دست میآید. اگر منحنی گویا باشد، آنها در مختصات همگن و k = d + 1 داده میشوند. اگر منحنی چند جملهای باشد، اینها به مختصات دکارتی داده میشوند. و k = d. |
شرح
BSplineCurve یک منحنی کلی اسپلاین را با استفاده از توابع پایه B-spline توصیف می کند. Splines در این فرم اغلب به عنوان B-Splines نامیده می شود.
منحنی spline درجه p با تعریف می شود
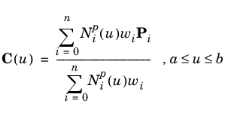
که در آن P i نقاط کنترل هستند، w i وزن ها، و N i p توابع پایه درجه B-spline هستند که در بردار گره غیر تناوبی و غیر یکنواخت تعریف شده اند.
برای N i p ( u ) از تعریف زیر استفاده می شود:
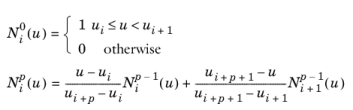
برای خطوط B غیر منطقی، همه وزن ها برابر با 1 هستند و منحنی را می توان به صورت بیان کرد
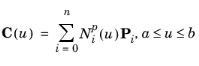
نقاط کنترل همگن Pw[i] که در سریال سازی یک منحنی منطقی استفاده می شود دارای اجزای زیر است:
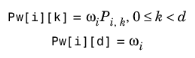
یک منحنی چند جمله ای همه وزن ها برابر با 1 است.
مثال
کلاس 12 BSplineCurve #
نسخه 2 #
3 #خیر
0 # منطقی؟
0 # دوره ای؟
3 # درجه
#وکتور گره
8 0 0 0 0 1 1 1 1 1
# نقطه کنترل
1 0 0
1 0.33333333333333333 0
1 0.66666666666666666 0.33333333333333333
1 1 1
همچنین ببینید
BezierCurve




